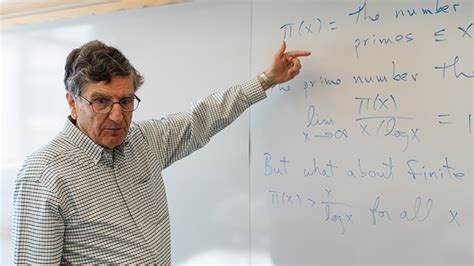Top 70 Theorems Quotes & Sayings

Men propound mathematical theorems in besieged cities, conduct metaphysical arguments in condemned cells, make jokes on the scaffold, discuss a new poem while advancing to the walls of Quebec, and comb their hair at Thermopylae. This is not panache; it is our nature.

We often hear that mathematics consists mainly of "proving theorems." Is a writer's job mainly that of "writing sentences?"

Theorems are fun especially when you are the prover, but then the pleasure fades. What keeps us going are the unsolved problems.

When a truth is necessary, the reason for it can be found by analysis, that is, by resolving it into simpler ideas and truths until the primary ones are reached. It is this way that in mathematics speculative theorems and practical canons are reduced by analysis to definitions, axioms and postulates.

Abstract ideas like equality and liberty have a spurious transparency, and can be used to derive pleasing theorems in the manner of Jean-Jacques Rousseau or John Rawls.

It is a matter for considerable regret that Fermat, who cultivated the theory of numbers with so much success, did not leave us with the proofs of the theorems he discovered. In truth, Messrs Euler and Lagrange, who have not disdained this kind of research, have proved most of these theorems, and have even substituted extensive theories for the isolated propositions of Fermat. But there are several proofs which have resisted their efforts.

The product of mathematics is clarity and understanding. Not theorems, by themselves. ... In short, mathematics only exists in a living community of mathematicians that spreads understanding and breathes life into ideas both old and new.

Less depends upon the choice of words than upon this, that their introduction shall be justified by pregnant theorems.

There are three signs of senility. The first sign is that a man forgets his theorems. The second sign is that he forgets to zip up. The third sign is that he forgets to zip down.

Phyllis explained to him, trying to give of her deeper self, 'Don't you find it so beautiful, math? Like an endless sheet of gold chains, each link locked into the one before it, the theorems and functions, one thing making the next inevitable. It's music, hanging there in the middle of space, meaning nothing but itself, and so moving...'

There are very few theorems in advanced analysis which have been demonstrated in a logically tenable manner. Everywhere one finds this miserable way of concluding from the special to the general and it is extremely peculiar that such a procedure has led to so few of the so-called paradoxes.

Without computers we will be stuck only proving theorems that have short proofs.

I am persuaded that this method [for calculating the volume of a sphere] will be of no little service to mathematics. For I foresee that once it is understood and established, it will be used to discover other theorems which have not yet occurred to me, by other mathematicians, now living or yet unborn.

Unlike mathematical theorems, scientific results can't be proved. They can only be tested again and again, until only a fool would not believe them. I cannot prove that electrons exist..........if you don't believe in them I have a high voltage cattle prod I'm willing to apply as an argument on their behalf. Electrons speak for themselves.

In science, every question answered leads to 10 more. I love that science can never, ever be finished. From a young age, people think, 'Science is hard and boring.' We don't tell children, 'Yes, you have to learn these formulae and theorems, but then you go on to learn about nuclear reactions and stars.'

Math does come easily to me, but I was always much more interested in what theorems imply about the world than in proving them.

The Three Theorems of Psychohistorical Quantitivity: The population under scrutiny is oblivious to the existence of the science of Psychohistory. The time periods dealt with are in the region of 3 generations. The population must be in the billions (±75 billions) for a statistical probability to have a psychohistorical validity.

What exactly is mathematics? Many have tried but nobody has really succeeded in defining mathematics; it is always something else. Roughly speaking, people know that it deals with numbers, figures, with relations, operations, and that its formal procedures involving axioms, proofs, lemmas, theorems have not changed since the time of Archimedes.

I approached the bulk of my schoolwork as a chore rather than an intellectual adventure. The tedium was relieved by a few courses that seem to be qualitatively different. Geometry was the first exciting course I remember. Instead of memorizing facts, we were asked to think in clear, logical steps. Beginning from a few intuitive postulates, far reaching consequences could be derived, and I took immediately to the sport of proving theorems.

I think that mathematics can benefit by acknowledging that the creation of good models is just as important as proving deep theorems.

All theorems have three names: a French name, a German name, and a Russian name, each nationality having claimed to discover it first. Once in a while there's an English name, too, but it's always Newton.

He knew by heart every last minute crack on its surface. He had made maps of the ceiling and gone exploring on them; rivers, islands, and continents. He had made guessing games of it and discovered hidden objects; faces, birds, and fishes. He made mathematical calculations of it and rediscovered his childhood; theorems, angles, and triangles. There was practically nothing else he could do but look at it. He hated the sight of it.

If only I had the Theorems! Then I should find the proofs easily enough.

I have found a very great number of exceedingly beautiful theorems.

God has the Big Book, the beautiful proofs of mathematical theorems are listed here.

To many, mathematics is a collection of theorems. For me, mathematics is a collection of examples; a theorem is a statement about a collection of examples and the purpose of proving theorems is to classify and explain the examples.

A peculiarity of the higher arithmetic is the great difficulty which has often been experienced in proving simple general theorems which had been suggested quite naturally by numerical evidence.

You can learn to find unknowns in equations, draw equidistant lines and demonstrate theorems, but in real life there's nothing to position, calculate, or guess.

I compare arithmetic with a tree that unfolds upwards in a multitude of techniques and theorems while the root drives into the depths.

If all sentient beings in the universe disappeared, there would remain a sense in which mathematical objects and theorems would continue to exist even though there would be no one around to write or talk about them. Huge prime numbers would continue to be prime, even if no one had proved them prime.

The Mean Value Theorem is the midwife of calculus - not very important or glamorous by itself, but often helping to deliver other theorems that are of major significance.

Now, one of my beliefs, one of my theorems that I have evolved over the years is that when it comes to Democrats and the media they will always tell us who they fear. And all we have to do to learn that is look at who they're trying to damage and/or destroy.

Mathematics is not arithmetic. Though mathematics may have arisen from the practices of counting and measuring it really deals with logical reasoning in which theorems-general and specific statements-can be deduced from the starting assumptions. It is, perhaps, the purest and most rigorous of intellectual activities, and is often thought of as queen of the sciences.

Paul Erdos has a theory that God has a book containing all the theorems of mathematics with their absolutely most beautiful proofs, and when he wants to express particular appreciation of a proof he exclaims, "This is from the book!"

The pursuit of pretty formulas and neat theorems can no doubt quickly degenerate into a silly vice, but so can the quest for austere generalities which are so very general indeed that they are incapable of application to any particular.

Papers should include more side remarks, open questions, and such. Very often, these are more interesting than the theorems actually proved. Alas, most people are afraid to admit that they don't know the answer to some question, and as a consequence they refrain from mentioning the question, even if it is a very natural one. What a pity! As for myself, I enjoy saying 'I do not know'.

The fundamental laws of the universe which correspond to the two fundamental theorems of the mechanical theory of heat. 1. The energy of the universe is constant. 2. The entropy of the universe tends to a maximum.

A dozen more questions occurred to me. Not to mention twenty-two possible solutions to each one, sixteen resulting hypotheses and counter-theorems, eight abstract speculations, a quadrilateral equation, two axioms, and a limerick. That's raw intelligence for you.

We decided that 'trivial' means 'proved'. So we joked with the mathematicians: We have a new theorem- that mathematicians can prove only trivial theorems, because every theorem that's proved is trivial.

I believe that mathematical reality lies outside us, that our function is to discover or observe it, and that the theorems which we prove, and which we describe grandiloquently as our "creations," are simply the notes of our observations.

Theorems often tell us complex truths about the simple things, but only rarely tell us simple truths about the complex ones. To believe otherwise is wishful thinking or "mathematics envy."

An axiomatic system establishes a reverberating relationship between what a mathematician assumes (the axioms) and what he or she can derive (the theorems). In the best of circumstances, the relationship is clear enough so that the mathematician can submit his or her reasoning to an informal checklist, passing from step to step with the easy confidence the steps are small enough so that he cannot be embarrassed nor she tripped up.

Mathematicians can and do fill in gaps, correct errors, and supply more detail and more careful scholarship when they are called on or motivated to do so. Our system is quite good at producing reliable theorems that can be solidly backed up. It's just that the reliability does not primarily come from mathematicians formally checking formal arguments; it comes from mathematicians thinking carefully and critically about mathematical ideas.

Theorems are not to mathematics what successful courses are to a meal.

A mathematician is a device for turning coffee into theorems.

That's the problem with false proofs of true theorems; it's not easy to produce a counterexample.

Young men should prove theorems, old men should write books.

The theory of numbers, more than any other branch of mathematics, began by being an experimental science. Its most famous theorems have all been conjectured, sometimes a hundred years or more before they were proved; and they have been suggested by the evidence of a mass of computations.

Humans like to think of themselves as unusual. We've got big brains that make it possible for us to think, and we think that we have free will and that our behavior can't be described by some mechanistic set of theorems or ideas. But even in terms of much of our behavior, we really aren't very different from other animals.

How many theorems in geometry which have seemed at first impracticable are in time successfully worked out!

A mathematician is a person who can find analogies between theorems; a better mathematician is one who can see analogies between proofs and the best mathematician can notice analogies between theories.

To a person of analytical ability, perceptive enough to realise that mathematical equipment was a powerful sword in economics, the world of economics was his or her oyster in 1935. The terrain was strewn with beautiful theorems begging to be picked up and arranged in unified order.

Isolated, so-called "pretty theorems" have even less value in the eyes of a modern mathematician than the discovery of a new "pretty flower" has to the scientific botanist, though the layman finds in these the chief charm of the respective sciences.

Mathematics does not grow through a monotonous increase of the number of indubitably established theorems but through the incessant improvement of guesses by speculation and criticism, by the logic of proofs and refutations.

There is a theorem that colloquially translates, You cannot comb the hair on a bowling ball. ... Clearly, none of these mathematicians had Afros, because to comb an Afro is to pick it straight away from the scalp. If bowling balls had Afros, then yes, they could be combed without violation of mathematical theorems.

For hundreds of pages the closely-reasoned arguments unroll, axioms and theorems interlock. And what remains with us in the end? A general sense that the world can be expressed in closely-reasoned arguments, in interlocking axioms and theorems.

Economists often like startling theorems, results which seem to run counter to conventional wisdom.

Mystery is an inescapable ingredient of mathematics. Mathematics is full of unanswered questions, which far outnumber known theorems and results. It's the nature of mathematics to pose more problems than it can solve. Indeed, mathematics itself may be built on small islands of truth comprising the pieces of mathematics that can be validated by relatively short proofs. All else is speculation.

There are infinitely many variations of the initial situation and therefore no doubt indefinitely many theorems of moral geometry.

Never call yourself a philosopher, nor talk a great deal among the unlearned about theorems, but act conformably to them. Thus, at an entertainment, don't talk how persons ought to eat, but eat as you ought. For remember that in this manner Socrates also universally avoided all ostentation.